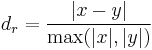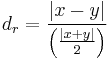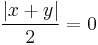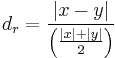Relative change and difference
The relative difference, percent difference, relative percent difference, or percentage difference between two quantities is the difference between them, expressed as a comparison to the size of one or both of them. Such measures are unitless numbers. Such measures are often used as a quantitative indicators of quality assurance and quality control for repeated measurements where the outcomes are expected to be the same. Similar terms are percentage change and relative change, which are ways to express a change in a variable compared to its starting value.
Contents |
Background
Percent difference is similar to another comparison technique called percent error, which is when one determines an experimental value and is comparing it to the accepted or actual value. Percent difference is different in that neither of the two values are assumed to be incorrect if there is a difference.
Formula
The percent difference of two experimental values, x1 and x2, can be calculated by dividing the absolute difference of the two values by the average value of the same two values as shown in the equation below:
 .
.
Both values (x1 and x2) must contain the same units in order to be compared correctly with one another. And as mentioned before, a zero percent difference is optimum and the higher the percent value, the less precision of the two values.
As the values are the result of an experiment, this formula has the advantage that if one of the values is zero, the result is still valid. The formula for percent error cannot be computed if the theoretical value is zero.
One final note to make is that a lot of confusion lies in mistakenly assuming that percent difference is the same as percent error. The difference is that percent difference is comparing two experimental values, whereas percent error compares one experimental value with the actual/accepted value.
Other approaches
One approach to obtain the relative difference of two numbers is their absolute difference divided by the maximum of the two numbers.
for at least one of the values not equal zero.
It is especially useful when comparing floating point values in programming languages for equality with a certain tolerance[1]. Another application is in the computation of approximation errors when the relative error of a measurement is required.
Another approach to obtain the relative difference of two numbers is their absolute difference divided by a standard value of the two numbers, e.g. their arithmetic mean:
This approach is often used when the two numbers reflect a change in some single underlying entity. Again, the relative difference is a unitless number expressed as a fraction.
A problem with the above approach is that if x and y have the same magnitude but opposite sign, then
which causes division by 0. So it may be better to replace the denominator with the average of the absolute values of x and y:
Percent error
The general standard of calculating the percent error involves using the absolute difference of the experimental (measured) and theoretical (accepted) values. Then take the difference and divide it by the theoretical (accepted) value to get percent error,
 .
.
The terms "Experimental" and "Theoretical" used in the equation above are commonly replaced with other similar terms. Other terms used for "experimental" could be measured or calculated and other terms used for "theoretical" could be actual or accepted. Either way, don't let the varying word choices confuse value assignment in the equation. Experimental value is what someone derived by use of calculation and measurement and would like to test its accuracy with the theoretical value, a value that is accepted by a scientific community or a value that could be seen as a goal for a successful result.
By using absolute functions in the percent error equation, we understand that the solution will always be a positive percent value. However, in the academic arena, it can be beneficial to remove the absolute function so as to provide more information to the result. Therefore, if a experimental value is less than the theoretical value, the percent error will be negative. This negative result lets the author and reader know more information about the experimental result. For example, experimentally calculating the speed of light and coming up with a negative percent error tells us that the experimental value is a velocity that is less than the speed of light. This is a big difference to getting a positive percent error, which means the experimental value is a velocity that is greater than the speed of light (violating the theory of relativity).
So rewriting the percent error equation by removing the absolute function, we have,
Without the use of the absolute function, it's important to note that the two values in the numerator are not commutative due to the use of subtraction without the absolute function. Therefore, it must remain as shown above: subtract the theoretical value from the experimental value and not vice versa.
Percentage change
A percentage change is a way to express a change in a variable. It represents the relative change between the old value and the new one.
For example, if a house today is worth $100,000 and the year after its worth goes up to $110,000, the percentage change of its worth can be expressed as
It can then be said that the worth of the house went up by 10%.
More generally, if V1 represents the old value and V2 the new one,
When the variable in question is a percentage itself, it is better to talk about its change by using percentage points, to avoid confusion between relative difference and absolute difference.
Note you would need to use an absolute value for V1 in the denominator regarding values with V1 being a negative and V2 being positive, as well as V1 being negative, and V2 being greater than V1 but still negative.
Examples
Comparing different groups
Let's look at a group of people, some males and some females. Here are the percentages of each subgroup that enjoy watching a particular TV show:
Males 35% Females 75%
The absolute difference is 40 percentage points (75% − 35%). The relative differences can be stated several ways:
47% = 35%/75% Males enjoy the TV show 47% less frequently than females. Or, about half as often as females.
214% = 75%/35% Females enjoy the TV show 214% more frequently than males. Or, over twice as often as males.
As ratios:
0.47 = 35/75 Males relative to females. 2.14 = 75/35 Females relative to males.
As percentages:
47% = 35/75 Males relative to females. 214% = 75/35 Females relative to males.
Characterizing change
Now let's look at a group of genderless Martians, before and after watching that TV show. The percentages of the group favorable to Earthlings are
Before 75% After 35%
The absolute difference is −0.4 or −40% (35% − 75%), e.g. Martian favorability to Earthlings decreased by 40 percentage points after watching the show. The relative difference (−0.4/0.75) can also be stated as a ratio (−0.53) or as a percentage (−53%), e.g. Martian favorability to Earthlings decreased 53% after watching the show.
See also
References
- "Understanding Measurement and Graphing". North Carolina State University. 2008-08-20. http://www.physics.ncsu.edu/courses/pylabs/205N_208N_MeasurementandErrors.pdf. Retrieved 2010-05-05.
- Hester, Jerry (2006-01-27). "Physics Tutorial: %Error and %Difference". Clemson University. http://phoenix.phys.clemson.edu/tutorials/error/index.html. Retrieved 2010-05-05.
- "Percent Difference – Percent Error". Illinois State University, Dept of Physics. 2004-07-20. http://www.phy.ilstu.edu/slh/Percent%20Difference%20Error.pdf. Retrieved 2010-05-05.